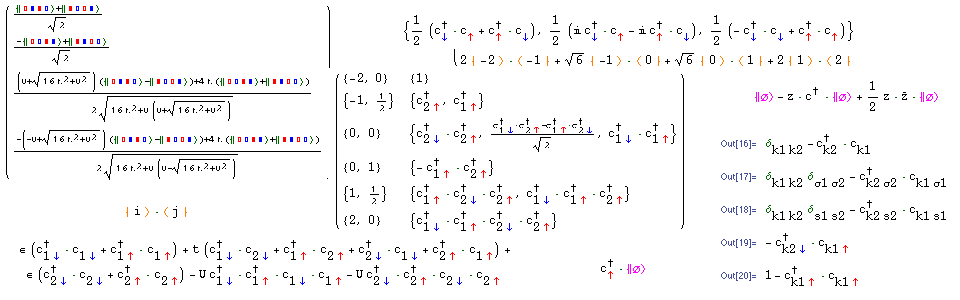
SNEG library
SNEG library is a
Mathematica package that provides a framework for performing
calculations using the operators of the second quantization
with an emphasis on the anti-commuting fermionic operators in the
context of solid-state and
atomic physics. It consists of a collection of transformation
rules that define the algebra of operators and a comprehensive library
of utility functions. The cornerstone of SNEG is a definition of non-commutative
multiplication with
automatic reordering of operators in a standard form (usually the
conventional normal ordering with creation operators preceding the
annihilation operators), which takes into account selected (anti)commutation
rules. Standard form reordering allows simplifications of expressions and
the choice of normal ordering permits efficient evaluation of matrix
elements in a given basis.
The library makes otherwise tedious calculations a routine operation.
Especially, it prevents inauspicious sign errors
when commuting fermionic operators.
Examples
Note: you need to have
Mathematica
or
Mathematica Player
installed in order to view the following examples.
Additional examples can be found in the Further examples sections
of the Help notebooks for SNEG functions. See also
Quick start manual in the form of Mathematica
notebook.
News
-
19.4.2022: updated version (2.0.0). The sneg code is now hosted
on
 github. This version
also fixes a bug in snegrealconstants (thanks for spotting this one, Luka!), and adds some new functions. There
is also a citable
github. This version
also fixes a bug in snegrealconstants (thanks for spotting this one, Luka!), and adds some new functions. There
is also a citable
 Zenodo snapshot.
Zenodo snapshot.
-
24.1.2019: updated version (1.250). Maintenance release, tested to
work with Mathematica 11.3.
-
29.7.2011:
SNEG - Mathematica package for symbolic calculations with
second-quantization-operator expressions, R. Zitko,
Comp. Phys. Comm. 182 2259, (2011) has been published.
 (PDF).
Please cite this work if you make extensive use of SNRG in your research.
(PDF).
Please cite this work if you make extensive use of SNRG in your research.
-
18.3.2011: updated version (1.228). Maintenance release,
tested to be compatible with Mathematica 7 and 8.
-
9.4.2008: updated version (1.191). It improves compatibility
with Mathematica 6 and adds support for spin operators.
Otherwise version 1.191 is only a minor update.
-
6.6.2007: updated version (1.168). In addition to much improved
documentation (now fully integrated in Mathematica Help Browser) and
additional examples, a considerable number of new features has been implemented.
-
14.7.2006: first public release of the library.
Features
-
Collection of utility functions that generate various operator expressions,
such as electron number, electron spin and isospin, one-electron and
two-electron hopping, projection operators, spin-spin and charge-charge
inter-site coupling, etc. This is heavily used in the "NRG
Ljubljana" for building expressions for the Hamiltonian and other
operators.
-
Manipulation of operator expressions: canonic conjugation, spin inversion.
-
Calculation of vacuum expectation values of operator expressions
- Occupation-number representation of states and evaluation of
operator-vector expressions. Occupation-number representations allows great
speed-up in applying a string of operators on a basis state.
-
Transformations from product-of-operators to occupation-number
representations of states and vice-versa
-
Generation of basis states with well-defined particle number Q and
spin projection Sz, well-defined number Q and spin S,
or well-defined isospin I and spin S. For models with reflection symmetry, a
parity quantum number can also be introduced. These sets of basis states
are used in the "NRG Ljubljana" code to perform
exact diagonalizations in various invariant subspaces.
-
Utility functions for manipulating sets of basis states: conversions between
various representations, mapping a function to each state, transformations
of basis, merging several sets of basis states, orthogonalization, etc.
-
Generation of matrix representations of operators in a given basis
-
Support for free (dummy) indexes and summed-over indexes: it is easy to write multiple sums over wave-numbers
ki and spins σi. Automatic simplifications
can be performed in such sums, which take into account that multiple
summed-over indexes can be interchanged, etc.
-
Support for Dirac's bra-ket notation. It is used to represent
degrees of freedom in addition to the fermionic ones in the
"NRG Ljubljana, in particular phonons and spin.
Bra-ket notation can be intermixed with the second-quantization operators
notation.
-
Distinction between particle and hole operators. This distinction is used in
the standard normal ordering (creation operators are those that create
a particle or a hole) and in the applications of the Wick theorem
(see next entry).
-
Simplifications using the Wick theorem, in particular calculation of the
ground state (vacuum) expectation values.
-
Support for commuting bosonic operators.
-
Support for anti-commuting Grassman variables and fermionic
coherent states.
-
Support for real (Majorana) fermions.
-
Automatic canonical ordering of fermionic operators in the case of
Fermi sea vacuum.
- Support for symbolic sums: automatic renaming of dummy indexes when
name conflicts appear, better simplification of expressions involving sums.
-
Automatic simplification of expressions with exponential functions of
operators using the Baker-Campbell-Hausdorff formula.
-
Built-in support for pretty printing of operator expressions,
obviating the need to use the Notation package.
Colors are used to further improve readability.
-
Code for rewritting an operator expression in terms of higher-level
functions, such as number, hopping, electron-electron repulsion, spin, etc.
operators.
-
Support for spin operators.
-
Functions for basis generation for some additional cases:
conserved total charge, conserved total spin, spinless fermions,
no conserved quantum numbers.
Applications
The SNEG library is useful beyond the NRG
calculations. It has been applied to perform exact
diagonalizations on Hubbard clusters,
perturbation theory
to higher orders and calculation of commutators of complex operator
expressions. It should also be suitable for educational purposes, since it
simplifies tedious calculations with second-quantization operators, much
like Mathematica eased learning calculus. A number of examples is included
in the SNEG library distribution; they can easily be extended to non-trivial
calculations.
Download
Download
the current
version of "sneg" from github (external link, zip file)
Installation: On macOS, copy sneg.m and, optionally,
Kernel/init.m, to
Library/Mathematica/Applications/sneg/
in your home directory.
On Linux, copy the archive contents to
.Mathematica/Applications/sneg/
in your home directory.
Please cite
R. Zitko,
Comp. Phys. Comm. 182 2259, (2011)
and  Zenodo snapshot.
if you make
extensive use of SNEG in your research.
Zenodo snapshot.
if you make
extensive use of SNEG in your research.
Older releases
SNEG version 1.250 (Jan 2019)
SNEG version 1.234 (Sep 2013)
SNEG version 1.232 (Nov 2012)
SNEG version 1.228 (March 2011)
SNEG version 1.191 (April 2008)
SNEG version 1.168 (January 2007)
SNEG version 1.76 (November 2006)
Last modified: 27.6.2022
Request more information
Rok Zitko's home page
 github. This version
also fixes a bug in snegrealconstants (thanks for spotting this one, Luka!), and adds some new functions. There
is also a citable
github. This version
also fixes a bug in snegrealconstants (thanks for spotting this one, Luka!), and adds some new functions. There
is also a citable
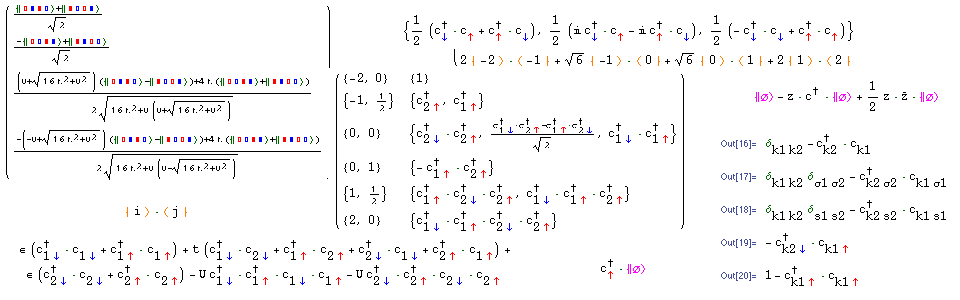
 github. This version
also fixes a bug in snegrealconstants (thanks for spotting this one, Luka!), and adds some new functions. There
is also a citable
github. This version
also fixes a bug in snegrealconstants (thanks for spotting this one, Luka!), and adds some new functions. There
is also a citable
Zenodo snapshot.
if you make
extensive use of SNEG in your research.